网络流学习1--最大流问题
前言
本来什么都不会的, 但是呢, 为了能顺利进入MSC in XDU去打ACM, 我就只能硬着头皮上啦…
网络流是什么
通俗的解释
什么是网络流呢???
某升专门去Google学术搜索了一下, 然后发现我什么也看不懂… 无奈翻出紫书开始研究, 用一个通俗的方式讲, 就是一张地图,许多城市, 不同城市间有道路, 但是为了防止事故, 都是单行道. 这些道路各有宽窄, 宽的路自然就运的东西多啦… 各个道路组成了一张道路交通网, 我们可以将其抽象化为网络这个词. 而网络流里面的流, 指的就是车辆运输的东西啦 ( 溜 ). 一条路所能承载的最大运输量, 称之为流量. 这大概就解释了一个十分清晰的网络流模型了…
最大流问题
解释
现在, 假设某升有天发达了在A市开了个仓库, 现在某升希望从A市向很远的B市运输东西, 但是呢, 每跑一次都要花费大量的人力物力, 所以需要找到一条路, 使得从A市到B市的一次运输能尽可能多的带东西过去.. 现在需要找到一条道路, 并求出理论上能运输的物品的最大数量…
第一次看这种问题感觉似乎不是很难? 广度优先搜索应该可以搞定吧 ( 汗 )…
概念
我们可以画一张简单的图:
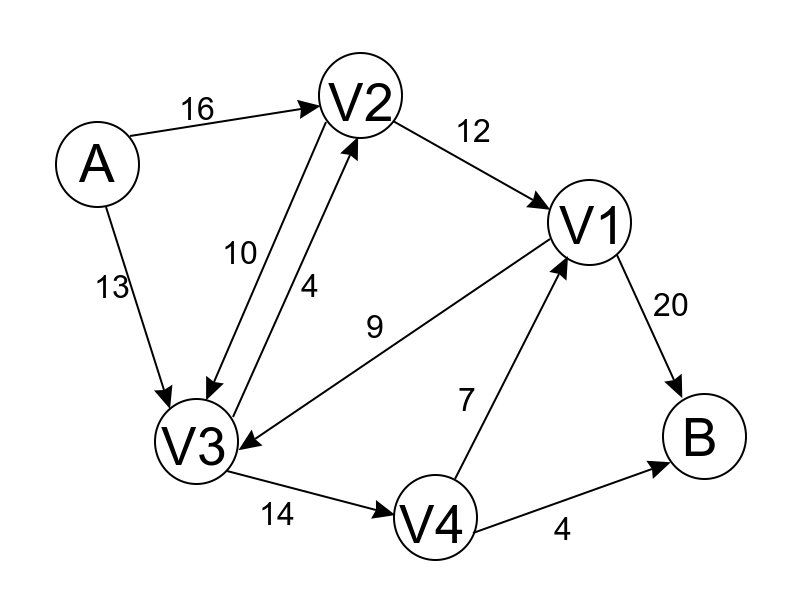
这张粗陋的图简单的写了一下刚刚某升运货的情况… 从A市到B市间隔了V1~V4四座城市, 某升可以在这里稍作停留. 问走哪条路才是最佳的选择呢? 在这张图里, 对于一条道路(u, v), 我们把它的运输上限称为容量(Capacity), 记为c(u, v), 把实际能运送的物品叫做流量(Flow), 记为f(u, v). 我们还可以发现A只出不进, B只进不出, 而其他的节点都会有进出. 在问题之中, 应当明确, 当运输任务完成时, A的输出量就是B的输入量 ( 否则某升就亏大了..
增广路算法
介绍
既然了解了这个问题, 就得想办法去解决它… 怎么解决呢? 这里有一种叫做增广路算法的东西.. 具体做法, 就是先建一个空图, 然后从零流量开始, 不断地增加流量, 保证每次增加之后都满足对于每条路: f(u, v) == -f(v, u), 每条路上的流量不超过路容量, 以及A市输出和B市输入是一致的. 这三个特性分别称为 斜对称性, 容量限制, 流量平衡.
我们把每条边上的容量和流量之差称之为残量, 就是残余容量的意思, 这样的话残量网络就会多出几条返回的道路.
现在我们可以发现一个惊人的事实: 残量网络中任何一条从A市到B市的道路都对应原来网络中一条增广路—意思就是只要求出所有可行道路中的最小残量d , 把所有边上的流量增加d即可. 这个过程就叫增广!
只要残量网络中存在增广路, 那么流量就有继续增大的方法; 当然, 如果不存在增广路了, 那么就说明我们的算法达成目的了!
代码
好了, 了解了这么多, 我怎么写这个代码呢?
最先想到的毫无疑问是DFS啦… 找路径用DFS还不快? 但是…想不出来DFS写出来的代码应该怎么去增流和维护… 这样一来, 就算实现了, 似乎也很容易爆时间… 那我们换种方法.. 通过紫书上说的, 有种基于BFS的Edmonds-Karp算法, 对付数据不刁钻的题目很好用.. 等我把代码抄一遍…
##include <cstring>
##include <algorithm>
##include <iostream>
using namespace std;
const int INF = 0x7f7f7f7f;
int dis[2001], // 流量
head[2001],
nxt[600001], // 邻接表存储
before[600001],
value[600001], // 路的容量
S, T, // 源和汇
num[501], // 存储输入数组
n, k = 1, // n是用来存储数组长度的
flow[501]; // f用来存储流
int q[2001], h, t, p[2001], maxlen;
void push(int from, int to, int val)
{
k++; // 递增边的数量
nxt[k] = head[from]; // 然后设置
head[from] = k;
before[k] = to;
value[k] = val;
}
void link(int from, int to, int value)
{
push(from, to, value); // 正向建路
push(to, from, 0); // 反向建路, 这样以后回退起来计算着很方便
}
bool bfs()
{
memset(dis, 0, sizeof dis); // 首先初始化distance
dis[S] = 1;
h = t = 0;
q[++t] = S;
while (h < t)
{
++h;
for (int i = head[q[h]]; i; i = nxt[i])
if (value[i] && !dis[before[i]])
{
dis[before[i]] = dis[q[h]] + 1;
q[++t] = before[i];
if (before[i] == T)
return 1;
}
}
return 0;
}
int dfs(int x, int flow)
{
if (x == T || !flow)
return flow;
int used = 0;
for (int i = p[x]; i; i = nxt[i])
if (value[i] && dis[before[i]] == dis[x] + 1)
{
int w = dfs(before[i], min(flow - used, value[i]));
value[i] -= w;
value[i ^ 1] += w;
used += w;
if (w)
p[x] = i;
if (used == flow)
return used;
}
if (!used)
dis[x] = 0;
return used;
}
int main()
{
cin >> n;
S = 0, T = n * 2 + 1; // 把汇设置成了两倍加一
for (int i = 1; i <= n; i++)
cin >> num[i];
for (int i = 1; i <= n; i++)
{
for (int j = 1; j < i; j++)
if (num[j] <= num[i] && flow[j] > flow[i])
flow[i] = flow[j];
flow[i]++;
maxlen = max(maxlen, flow[i]);
} // 建流
//接下来使用上述介绍的方法建图
cout << maxlen << endl;
for (int i = 1; i <= n; i++)
link(i, i + n, 1);
for (int i = 1; i <= n; i++)
if (flow[i] == 1)
link(S, i, 1);
for (int i = 1; i <= n; i++)
if (flow[i] == maxlen)
link(i + n, T, 1);
for (int i = 1; i <= n; i++)
for (int j = 1; j < i; j++)
if (num[j] <= num[i] && flow[j] == flow[i] - 1)
link(j + n, i, 1); // 建图完毕
int ans = 0;
while (bfs())
{
memcpy(p, head, sizeof(p));
ans += dfs(S, INF);
}
cout << ans << endl;
link(1, 1 + n, INF), link(S, 1, INF);
if (flow[n] == maxlen)
link(n + n, T, INF), link(n, n * 2, INF);
while (bfs())
{
memcpy(p, head, sizeof(p));
ans += dfs(S, INF);
}
cout << ans << endl;
}